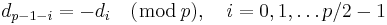Table of simple cubic graphs

The connected 3-regular (cubic) simple graphs are listed for small vertex numbers.

1 Connectivity
2 LCF notation
3 Table
4 Vector coupling coefficients
5 See also
6 References

Connectivity

The count of simple cubic graphs is 1, 2, 5, 19,... for 2, 4, 6, 8,... vertices (sequence A002851 in OEIS). A classification according to edge connectivity is made as follows: the 1-connected and 2-connected graphs are defined as usual. This leaves the other graphs in the 3-connected class because each 3-regular graph can be split by cutting all edges adjacent to any of the vertices. To refine this definition in the light of the algebra of coupling of angular momenta (see below), a subdivision of the 3-connected graphs is helpful. We shall call

Non-trivially 3-connected those that can be split by 3 edge cuts into sub-graphs with at least two vertices remaining in each part
Cyclically 4-connected—all those not 1-connected, not 2-connected, and not non-trivially 3-connected

This declares the numbers 3 and 4 in the first column of the tables below.

LCF notation

The LCF notation is a notation by Joshua Lederberg, Coxeter and Frucht, for the representation of cubic graphs that are Hamiltonian.

The two edges along the cycle adjacent to any of the vertices are not written down.

Let $v$ be the vertices of the graph and describe the Hamiltonian circle along the $p$ vertices by the edge sequence $v 0 v 1,v 1 v 2, ... ,v p-2 v p-1,v p-1 v 0$ . Halting at a vertex $v i$ , there is one unique vertex $v j$ at a distance $d i$ joined by a chord with $v i$ ,

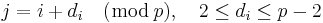$j=i%2Bd_i\quad (\bmod\, p),\quad 2\le d_i\le p-2$ .

The vector $[d 0,d 1, ..., d p-1]$ of the $p$ integers is a suitable, although not unique, representation of the cubic Hamiltonian graph. This is augmented by two additional rules:

If a $d i >p/2$ , replace it by $d i -p$ ;
avoid repetition of a sequence of $d i$ if these are periodic and replace them by an exponential notation.

Since the starting vertex of the path is of no importance, the numbers in the representation may be cyclically permuted. If a graph contains different Hamiltonian circuits, one may select one of these to accommodate the notation. The same graph may have different LCF notations, depending on precisely how the vertices are arranged.

Often the anti-palindromic representations with

$d_{p-1-i}= -d_i \quad (\bmod\,p), \quad i=0,1,\ldots p/2-1$

are preferred (if they exist), and the redundant part is then replaced by ";-". The LCF notation $[5,-9,7,-7,9,-5] 4$ , for example, and would at that stage be condensed to $[5,-9,7;-] 4$ .

Table

4 nodes

connectivity	LCF	names
4	[2]^4	K₄

6 nodes

connectivity	LCF	names
3	[2,3,-2]^2	W_n,2, prism graph Y₃
4	[3]^6	K_3,3

8 nodes

connectivity	LCF	names
2	[2,2,-2,-2]^2
3	[4,-2,4,2]^2 or [2,3,-2,3;-]
3	[2,4,-2,3,3,4,-3,-3]
4	[-3,3]^4	cubical graph
4	[4]^8 or [4,-3,3,4]^2	Wagner graph

10 nodes

connectivity	LCF	names
1		Edge list 0-1,0-6,0-9,1-2,1-5,2-3,2-4,3-4,3-5,4-5,6-7,6-8,7-8,7-9,8-9
2	[4,2,3,-2,-4,-3,2,2,-2,-2]
2	[3,3,3,-3,-3,-3,2,2,-2,-2]
2	[2,3,-2,2,-3,-2,2,2,-2,-2]
2	[2,2,-2,-2,5]^2
3	[2,3,-2,5,-3]^2
3	[2,-4,-2,5,2,4,-2,4,5,-4]
3	[5,3,5,-4,-3,5,2,5,-2,4]
3	[-4,3,3,5,-3,-3,4,2,5,-2]
3	[3,-3,5,-3,2,4,-2,5,3,-4]
3	[-4,4,2,5,-2]^2
3	[5,-2,2,4,-2,5,2,-4,-2,2]
3	[2,5,-2,5,5]^2
3	[5,-3,-3,3,3]^2
4	[5,-4,4,-4,4]^2
4	[5,-4,4,5,5]^2
4	[5]^10
4	[-4,4,-3,5,3]^2
4		Petersen graph

12 nodes

connectivity	LCF	names
1		Edge list 0-1,0-2,0-11,1-2,1-6,2-3,3-4,3-5,4-5,4-6,5-6,7-8,7-9,7-11,8-9,8-10,9-10,10-11
1		Edge list 0-1,0-6,0-11,1-2,1-3,2-3,2-5,3-4,4-5,4-6,5-6,7-8,7-9,7-11,8-9,8-10,9-10,10-11
1		Edge list 0-1,0-3,0-11,1-2,1-6,2-3,2-5,3-4,4-5,4-6,5-6,7-8,7-9,7-11,8-9,8-10,9-10,10-11
1		Edge list 0-1,0-6,0-11,1-2,1-4,2-3,2-5,3-4,3-6,4-5,5-6,7-8,7-9,7-11,8-9,8-10,9-10,10-11
2	[4,2,3,-2,-4,-3]^2
2	[4,2,3,-2,-4,-3,3,3,3,-3,-3,-3]
2	[4,2,3,-2,-4,-3,2,3,-2,2,-3,-2]
2	[3,3,3,-3,-3,-3]^2
2	[3,3,3,-3,-3,-3,2,3,-2,2,-3,-2]
2	[2,3,-2,2,-3,-2]^2
2	[6,2,3,-2,3,-3,6,-3,2,2,-2,-2]
2	[6,3,3,4,-3,-3,6,-4,2,2,-2,-2]
2	[4,2,3,-2,-4,-3,5,2,2,-2,-2,-5]
2	[3,3,3,-3,-3,-3,5,2,2,-2,-2,-5]
2	[2,3,-2,2,-3,-2,5,2,2,-2,-2,-5]
2	[5,2,4,-2,3,-5,-4,-3,2,2,-2,-2]
2	[3,4,4,-3,3,-4,-4,-3,2,2,-2,-2]
2	[2,4,-2,4,2,-4,-2,-4,2,2,-2,-2]
2	[2,2,-2,-2,-5,5]^2
2	[4,5,3,4,-4,-3,-5,-4,2,2,-2,-2]
2	[5,2,-3,-2,6,-5,2,2,-2,-2,6,3]
2	[2,4,-2,3,3,-4,-3,-3,2,2,-2,-2]
2	[2,2,-2,-2,5,3,5,3,-3,-5,-3,-5]
2	[2,2,-2,-2,6,6]^2
2	[6,-2,2,2,-2,-2,6,2,2,-2,-2,2]
2	[-2,3,-3,2,-3,-2,2,2,-2,-2,2,3]
2	[2,2,-2,-2,5,2,5,-2,2,-5,-2,-5]
2	[-2,-2,2,2]^3
3	[2,3,-2,3,-3,3,-3;-]
3	[2,3,-2,3,-3,4,-3,3,3,-4,-3,-3]
3	[2,3,-2,3,-3,4,-3,4,2,-4,-2,-4]
3	[2,4,-2,3,4,-4,-3,3,-4,2,-3,-2]
3	[2,4,-2,3,5,-4,-3,3,3,-5,-3,-3]
3	[2,4,-2,3,6,-4,-3,2,3,-2,6,-3]
3	[-5,2,-3,-2,6,3,3,5,-3,-3,6,3]
3	[-4,2,-3,-2,6,2,3,-2,4,-3,6,3]
3	[3,4,4,-3,4,-4,-4,3,-4,2,-3,-2]
3	[3,4,4,-3,5,-4,-4,3,3,-5,-3,-3]
3	[6,3,3,6,-3,-3]^2
3	[2,5,-2,2,4,-2,-5,3,-4,2,-3,-2]	Frucht graph
3	[2,5,-2,2,5,-2,-5,3,3,-5,-3,-3]
3	[2,5,-2,2,6,-2,-5,2,3,-2,6,-3]
3	[3,5,3,-3,4,-3,-5,3,-4,2,-3,-2]
3	[3,5,3,-3,5,-3,-5,3,3,-5,-3,-3]
3	[3,6,4,-3,6,3,-4,6,-3,2,6,-2]
3	[-4,4,2,-4,-2,-4;-]
3	[-4,4,-3,3,6,-4,-3,2,4,-2,6,3]
3	[-5,2,6,-2,5,6,4,5,6,-5,-4,6]
3	[-5,2,4,-2,6,3,-4,5,-3,2,6,-2]
3	[-4,2,3,-2,5,-3,5,3,4,-5,-3,-5]
3	[2,6,-2,3,4,5,-3,6,-4,2,-5,-2]
3	[2,-5,-2,4,5,6,4,-4,5,-5,-4,6]
3	[2,5,-2,4,-5,4,-5,-4,2,-4,-2,5]
3	[3,6,4,-3,4,5,-4,6,-4,2,-5,-2]
3	[3,5,5,-3,-5,4,-5,-5,2,-4,-2,5]
3	[-5,-2,3,-5,5,-3,2,5,-2,-5,5,2]
3	[-4,2,3,-2,6,-3,5,2,4,-2,6,-5]
3	[4,6,6,2,-4,-2]^2
3	[-5,3,3,5,-3,-3,4,5,-5,2,-4,-2]
3	[5,6,-4,3,4,-5,-3,6,-4,2,4,-2]
3	[-4,5,2,-4,-2,5;-]	Dürer graph
3	[2,5,-2,5,3,5,-5,-3,-5,2,-5,-2]
3	[2,-5,-2,3,5,6,-3,3,5,-5,-3,6]
3	[2,6,-2,5,2,5,-2,6,-5,2,-5,-2]
3	[6,-2,2]^4
3		Tietze's Graph
3	[2,6,-2,6]^3
4	[-3,3]^6
4	[3,6,6,-3,6,6]^2
4	[-4,4,-3,3,5,-4,-3,3,4,-5,-3,3]
4	[4,-5,-5,4,-4,6,4,-4,5,5,-4,6]
4	[4,-5,5,6,-4,5,5,-5,5,6,-5,-5]
4	[4,-4,6]^4
4	[6,-5,5]^4
4	[3,-5,5,-3,5,6,4,-5,5,-5,-4,6]
4	[5,-5,-3,4,5,-5,4,-4,5,-5,-4,3]
4	[-5,3,6,-5,-3,4,5,5,6,-4,5,-5]
4	[-3,6,4,-4,4,5,-4,6,-4,3,-5,4]
4	[5,6,6,-4,5,-5,4,6,6,-5,-4,4]
4	[-4,5,-4,4,-5,4,-5,-4,4,-4,4,5]
4	[-3,4,-3,5,3,-4,4,-3,-5,3,-4,3]
4	[-5,3,-3,5,-3,5,3,5,-5,-3,-5,3]
4	[5,-5,-3,3]^3	Franklin graph
4	[3,6,6,-3,-5,5]^2
4	[6,-5,-4,4,-5,4,6,-4,5,-4,4,5]

The LCF entries are absent above if the graph has no Hamiltonian cycle, which is rare (see Tait's conjecture). In this case a list of edges between pairs of vertices labeled 0 to n-1 in the third column serves as an identifier.

Vector coupling coefficients

Each 4-connected (in the above sense) simple cubic graph on 2n nodes defines a class of quantum mechanical 3n-j symbols. Roughly speaking, each vertex represents a 3-jm symbol, the graph is converted to a digraph by assigning signs to the angular momentum quantum numbers $j$ , the vertices are labelled with a handedness representing the order of the three $j$ (of the three edges) in the 3-jm symbol, and the graph represents a sum over the product of all these numbers assigned to the vertices.

There are 1 (6j), 1 (9j), 2 (12j), 5 (15j), 18 (18j), 84 (21j), 607 (24j), 6100 (27j), 78824 (30j), 1195280 (33j), 20297600 (36j), 376940415 (39j) etc. of these (sequence A175847 in OEIS).

If they are equivalent to certain vertex-induced binary trees (cutting one edge and finding a cut that splits the remaining graph into two trees), they are representations of recoupling coefficients, and are then also known as Yutsis graphs (sequence A111916 in OEIS).

References

Yutsis, A. P.; Levinson, I. B.; Vanagas, V. V.; Sen, A. (1962). Mathematical Apparatus of the theory of angular momentum. Israel program for scientific translations. http://ntrs.nasa.gov/search.jsp?R=491319&id=2&as=false&or=false&qs=N%3D4294964378%26Ns%3DHarvestDate%257c1.
Massot, J.-N.; El-Baz, E.; Lafoucriere, J. (1967). "A general graphical method for angular momentum". Reviews of Modern Physics 39 (2): 288–305. Bibcode 1967RvMp...39..288M. doi:10.1103/RevModPhys.39.288.
Frucht, R. (1977). "A canonical representation of trivalent Hamiltonian graphs". Journal of Graph Theory 1 (1): 45–60. doi:10.1002/jgt.3190010111. MR 0463029.
Clark, L.; Entringer, R. (1983). "Smallest maximally non-Hamiltonian graphs". Per. Mathem. Hungar. 14 (1): 57–68. doi:10.1007/BF02023582. MR 0697357.
Wormald, N. C. (1985). "Enumeration of cyclically 4-connected cubic graphs". Journal of Graph Theory 9: 563–573. doi:10.1002/jgt.3190090418. MR 0890248.
Bar-Shalom, A.; Klapisch, M. (1988). "NJGRAF - an efficient program for calculation of general recoupling coefficients by graphical analysis, compatible with NJSYM". Comp. Phys. Comm. 50 (3): 375–393. Bibcode 1988CoPhC..50..375B. doi:10.1016/0010-4655(88)90192-0.
Brinkmann, G. (1996). "Fast generation of cubic graphs". Journal of Graph Theory 23 (2): 139–149. doi:10.1002/(SICI)1097-0118(199610)23:2<139::AID-JGT5>3.0.CO;2-U. MR 1408342.
Fack, V.; Pitre, S. N.; Van der Jeugt, J. (1997). "Calculation of general recoupling coefficients using graphical methods". Comp. Phys. Comm. 101 (1–2): 155–170. Bibcode 1997CoPhC.101..155F. doi:10.1016/S0010-4655(96)00170-1.
Danos, M.; Fano, U. (1998). "Graphical analysis of angular momentum for collision products". Physics Reports 304 (4): 155–227. doi:10.1016/S0370-1573(98)00020-9.
Meringer, M. (1999). "Fast generation of regular graphs and construction of cages". Journal of Graph Theory 30 (2): 137–146. doi:10.1002/(SICI)1097-0118(199902)30:2<137::AID-JGT7>3.0.CO;2-G. MR 1665972.
Van Dyck, D.; Brinkmann, G.; Fack, V.; McKay, B. D. (2005). "To be or not to be Yutsis: Algorithms for the decision problem". Comp. Phys. Comm. 173 (1–2): 61–70. Bibcode 2005CoPhC.173...61V. doi:10.1016/j.cpc.2005.07.008. MR 2179511.
Van Dyck, D.; Fack, V. (2007). "On the reduction of Yutsis graphs". Disc. Math. 307 (11–12): 1506–1515. doi:10.1016/j.disc.2005.11.088. MR 2311125.
Aldred, R. E. L.; Van Dyck, D.; Brinkmann, G.; Fack, V.; McKay, B. D. (2009). "Graph structural properties of non-Yutsis graphs allowing fast recognition". Disc. Math. 157 (2): 377–386. doi:10.1016/j.dam.2008.03.020. MR 2479811.
Mathar, Richard J. (2011). "The Wigner graphs up to 12 Vertices". arXiv:1109.2358.